To understand the parallels between the thinking of Prussian military theorist Carl von Clausewitz (1780-1831) and that of the nonlinear mathematicians, see “Clausewitz, Nonlinearity and the Unpredictability of War,” by Alan D. Beyerchen (Department of History, Ohio State University), International Security, 17:3 (Winter, 1992). This is probably the most important article on Clausewitz since 1976. Also see our page "Clausewitz and Complexity," as well as the Clausewitz Bibliography on Nonlinearity on ClausewitzStudies.org.

PAGE CONTENTS:
Books
Lorenz Attractor (or "Strange Attractor")
Brownian motion
Double Pendulum
Randomly Oscillating Magnetic Pendulum
Logistic Map/Bifurcation Diagram
The Game of Life
Emergence
Complex Adaptive Systems
Afghan Stability
Longer videos on Complexity

See also these links to information on fractals.

Lorenz Attractor/"strange attractor"

Here (above) is an animated .gif of Edward Lorenz's "strange attractor." It describes a system very similar to Clausewitz's Trinity imagery, which has three attractors, but the Lorenz system may be especially relevant to Clausewitz's way of describing the dynamic variation in political and military objectives, i.e, the way that the opponents' interacting strategies tend to flip independently between 'limited' objectives and the objective of rendering the other player militarily and politically helpless. (See the very informative Wikipedia article, "Lorenz System," from which the image above was borrrowed.The Lorenz attractor does much to explain the "butterfly effect"—called in formal mathematics "sensitive dependence on initial conditions"—but its visual similarity to a butterfly is simply a strange coincidence.)

And there's a more modern demonstrator at https://highfellow.github.io/lorenz-attractor/attractor.html.

Einstein's Explanation of Brownian Motion

This animation demonstrates Brownian motion. Brownian motion is an old concept and does not really have anything to do with Chaos or Complexity per se—it really is random movement, though it can often look quite like it has some purpose or direction. The big particle can be considered as a dust particle while the smaller particles can be considered as molecules of a gas. On the left is the view one would see through a microscope. The purely physical explanation for the "random walk" of the dust particle is that the molecules of the dispersion medium, which move due to a wide variety of forces—convection, transient electrical fields, vibration induced from outside, even quantum events—strike the suspended particle from all sides with random direction and timing. The sum of all vectors and energies over time is reflected in the trajectory of the particle.

Double Pendulum

The animation above demonstrates deterministic chaos. Focus on the behavior of the red dot and imagine that you can't see the mechanism that moves it. This is an excellent way to demonstrate how complex behavior—even seemingly random behavior—can be created by very simple rules and systems. If you're paranoid about math-based animations, see the similar videos below of physical examples.

Double pendulum | Chaos | Butterfly effect | Computer simulation

This computer simulation shows how data generated by the pendulum can appear like totally random movement once you hide the mechanism itself. This illustrates the following quotation:

Don't tell me "There's no right explanation." There is a right explanation. We just can't know what it is.

Christopher Bassford

"Predictable Randomness." This is an interesting discussion of the difference between
"randomness" and "deterministic chaos."

Click the image above to go to a video of a live demonstration of a dual double pendulum. The double pendulum itself is an extremely simple system (there are only two points of freedom) that demonstrates deterministic chaos. The dual version (in which two double pendulums are suspended on the same axle) hows how dramatically the system's behavior can differ based on tiny differences in input (i.e., its sensitivity to initial conditions). (direct link).

Here is a link to an interactive Java applet on the double pendulum from the Virtual Physics Laboratory at Northwestern University.

Randomly Oscillating Magnetic Pendulum
(The image Clausewitz used to illustrate the Clausewitzian Trinity in Vom Kriege.)

Logistic Map/Bifurcation Diagram

The Game of Life

Invented in 1970 by John Horton Conway, Professor of Finite Mathematics at Princeton University. [This is discussed in Waldrop, Complexity—check the index for references. See also Daniel C. Dennett, Darwin's Dangerous Idea: Evolution and The Meanings of Life (New York: Simon & Schuster; Reprint edition, 1996), pp.166-176.] This simple mathematical exercise led investigators to a great many other ideas, but it also led directly to the entire field of "Artificial Life."

The Game of Life provides examples of "emergent complexity" and "self-organizing systems." It has a simple rule-set: "For each cell in the grid, count how many of its eight neighbors are ON at the present instant. If the answer is exactly two, the cell stays in its present state (ON or OFF) in the next instant. If the answer is precisely three, the cell is ON in the next instant whatever its current state. Under all other conditions, the cell is OFF." These basic rules were surprisingly hard to discover and seem to be unalterable or inevitable—that is, any other rules produce very uninteresting results: the system rapidly either freezes up solid or evaporates into nothingness. (Evidently, back in 1970 this game was more addictive to scientists than "Pong" was.)

Given this very simple rule (the only rule in the model universe we have created), the game demonstrates a surprising amount of complexity, depending on initial conditions. Click on these two screenshots from a computer-driven version of the game to see the very different system behaviors driven purely by the initial configuration of ON cells—um... What do we call that effect?)

Play the game yourself. Various Game of Life applications can be downloaded free from http://www.ibiblio.org/lifepatterns/. You'll have to install it on your own computer, of course.

See also http://www.math.com/students/wonders/life/life.html.

Emergence

Video (7.3 minutes): "Emergence—How Stupid Things Become Smart Together." Emergence is a key concept in Complexity—a major reason why it applies in so many different fields. After considering why systems built by "a whole buncha dumb critters interacting" can create something smart, we might want to consider why "a whole buncha intelligent humans interacting"—i.e., organizations—so frequently create disasters.

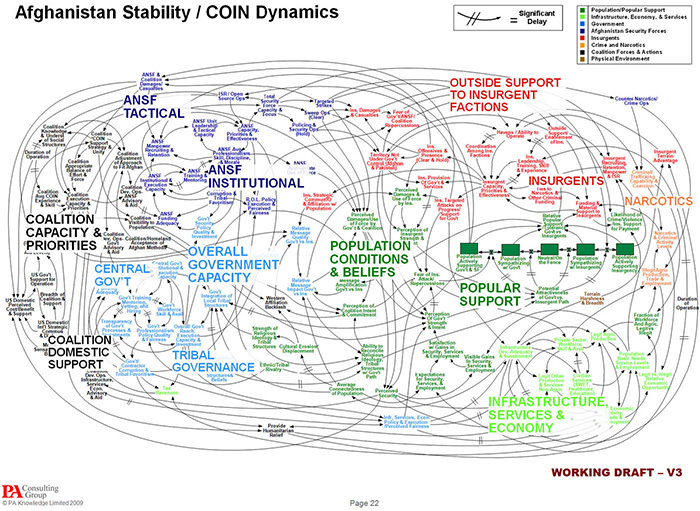
A Complex Adaptive System (CAS)

Although it may look like a street in India, this is actually the Westphalian state system.

Eric Berlow: "How Complexity Leads to Simplicity"
TED Global, 2010. Filmed July 2010. Posted on TED November 2010.
Original Url

Click the image below for a larger, reasonably high-resolution version of the Afghanistan graphic to which speaker Eric Berlow refers.

LONGER VIDEOS
(on Complexity broadly speaking, including the narrower field of Chaos)

James Gleick discussing his famous book Chaos: Making a New Science (New York: Penguin, 1987). Get the 20th anniversary edition (New York: Penguin, 2008), ISBN 9780143113454.

NOVA: "Hunting the Hidden Dimension."This is a one-hour video on fractals, divided into five chapters. This documentary highlights a host of filmmakers, fashion designers, physicians, and other researchers who are using fractal geometry to innovate and inspire. Also lots of textual material. Original PBS Broadcast Date: October 28, 2008. Also available on DVD from Amazon.com.

The Secret Life of Chaos (BBC 2010). Full Length Documentary. This video appears never to have been published by the BBC on DVD, but can be seen via the link above. You can find a great deal of video and information on it at http://atheistmovies.blogspot.com/2010/01/bbc-secret-life-of-chaos.html. Or try the DailyMotion posting. There is a low-bandwidth version of the video here.

CHAOS: A MATHEMATICAL ADVENTURE

This is a film about dynamical systems, the butterfly effect and chaos theory, intended for a wide audience. From Jos Leys, Étienne Ghys and Aurélien Alvarez, comes CHAOS, a math movie with nine 13-minute chapters. Available in a large choice of languages and subtitles. https://www.chaos-math.org/en/film.html. Great graphics and animations; the pace is oddly slow.

Return to top